
프로그래머스 Lv.2(JS) - 유사 칸토어 비트열
문제
문제 설명
수학에서 칸토어 집합은 0과 1 사이의 실수로 이루어진 집합으로, [0, 1]부터 시작하여 각 구간을 3등분하여 가운데 구간을 반복적으로 제외하는 방식으로 만들어집니다.
남아는 칸토어 집합을 조금 변형하여 유사 칸토어 비트열을 만들었습니다. 유사 칸토어 비트열은 다음과 같이 정의됩니다.
- 0 번째 유사 칸토어 비트열은 “1” 입니다.
- n(1 ≤ n) 번째 유사 칸토어 비트열은 n - 1 번째 유사 칸토어 비트열에서의 1을 11011로 치환하고 0을 00000로 치환하여 만듭니다.
남아는 n 번째 유사 칸토어 비트열에서 특정 구간 내의 1의 개수가 몇 개인지 궁금해졌습니다.
n과 1의 개수가 몇 개인지 알고 싶은 구간을 나타내는 l, r이 주어졌을 때 그 구간 내의 1의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤
n≤ 20 - 1 ≤
l,r≤ 5^n- l ≤
r<l+ 10,000,000 l과r은 비트열에서의 인덱스(1-base)이며 폐구간 [l, r]을 나타냅니다.
- l ≤
입출력 예
| n | l | r | result |
|---|---|---|---|
| 2 | 4 | 17 | 8 |
정답
풀이 코드
function solution(n, l, r) {
const calcBit = (index) => {
let exp = 0;
let result = 0;
while (index > 5 ** (exp + 1)) exp++;
if (exp === 0) return index < 3 ? index : index - 1;
const quotient = Math.floor(index / 5 ** exp);
const remainder = quotient + 1 !== 3 ? index % 5 ** exp : 0;
result += quotient >= 3 ? (quotient - 1) * 4 ** exp : quotient * 4 ** exp;
return result + calcBit(remainder);
};
return calcBit(r) - calcBit(l - 1);
}풀이 설명
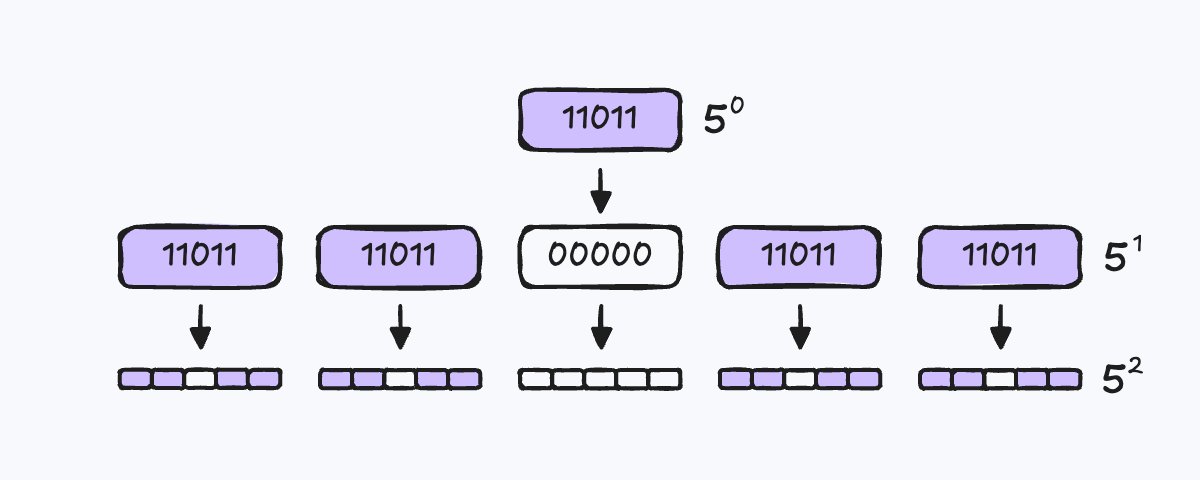
- 5n까지의 전체 비트열에서 1의 개수는 4n개입니다.
- 폐구간 [a, b]는 a와 b를 포함하는 사이 구간을 의미합니다.
const calcBit = (index) => {
let exp = 0;
let result = 0;
while (index > 5 ** (exp + 1)) exp++;
if (exp === 0) return index < 3 ? index : index - 1;
};calcBit는 0번 인덱스부터 주어진 index까지의 구간에서 1의 개수를 반환하는 재귀 함수입니다.
- 먼저
index보다 작거나 같은 5n 중 가장 큰n(=exp)값을 구합니다.
예를 들어index가 17이라면exp는 1입니다.(51 < 17 < 52)
index가 5 미만일 경우(exp===0)에는 전체 비트열이 11011이므로 아래와 같은 방법으로 처리합니다.
- index < 3 → 1의 개수는
index와 같습니다. - index >= 3 → 3번째는 항상 0이므로 1의 개수는
index-1
const calcBit = (index) => {
//...
const quotient = Math.floor(index / 5 ** exp);
const remainder = quotient + 1 !== 3 ? index % 5 ** exp : 0;
result += quotient >= 3 ? (quotient - 1) * 4 ** exp : quotient * 4 ** exp;
return result + calcBit(remainder);
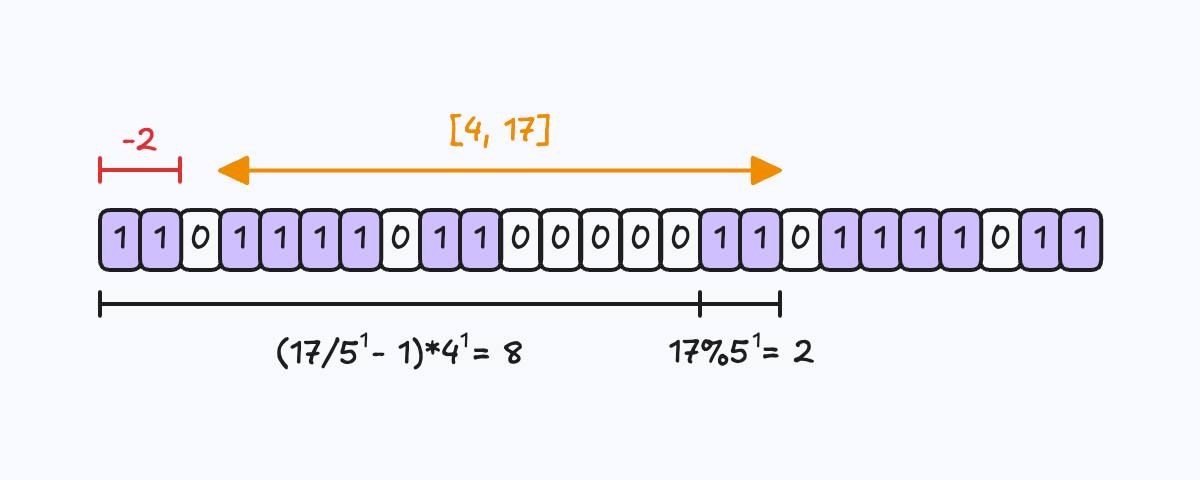
};quotient는 구간이 5개로 나뉘었을 때 index가 몇 번째 구간에 속하는지 나타냅니다.
remainder는 아래 두 가지 경우로 나눌 수 있습니다.
-
quotient가 2인 경우: 나머지는 항상 0이 되는 중앙 구간이므로 이후 탐색을 막기 위해 0을 저장합니다. -
그 외의 경우:
index를 5exp로 나눈 나머지를 저장합니다.
quotient가 3 이상인 경우, 중앙 구간(3번째)을 포함하므로 quotient - 1에 4exp를 곱합니다.
3 미만의 경우에는 단순히 quotient*4exp만큼 1이 존재합니다.
해당 값을 result에 누적하고 나머지 구간에 대해서는 calcBit를 재귀 호출합니다.
function solution(n, l, r) {
const calcBit = (index) => {
//...
};
return calcBit(r) - calcBit(l - 1);
}폐구간 [l, r]은 l과 r의 인덱스를 모두 포함하므로 0부터 r까지의 1의 개수에서 0부터 l-1까지의 1의 개수를 뺀 결과를 리턴합니다.